Maximum-Cut

Maximum-Cut is the problem of maximizing the weights of edges between different groups when partitioning into two subsets in a given vertex set of graph.

Simple Example

First, let’s we solve the maximum-cut of following simple graph.

data = """5 6
1 2 1
1 4 1
2 3 1
2 4 1
3 5 1
4 5 1
"""

import networkx
import matplotlib.pyplot as plt

# create networkx graph
G = networkx.Graph()
f = iter(data.split("\n"))
N, E = map(int, next(f).split())  # N is the number of vartexes, and E is the number of edges
for e in range(E):
    i, j, w = map(int, next(f).split())
    G.add_edge(i, j, weight=w)

# plot the graph
fig, ax = plt.subplots()
pos = {1: (0, 1), 2: (1, 2), 3: (2, 2), 4: (1, 0), 5: (2, 0)}
networkx.draw_networkx(G, pos, with_labels=True, node_color="white", edgecolors="black")
ax.set_title("Example simple Graph")

We divide these five vertexes into two groups, \(S\) and \(T\). We create and assign a spin variable \(s_i\) to the vertex \(i\) of the graph, where spin variable only takes +1 or -1. \(s_i = +1\) represents vertex \(i\) is in group \(S\), and \(s_i = -1\) represents vertex \(i\) is in group \(T\). This gives us that \((1 - s_i s_j)\) takes 0 only if vertex \(i\) and \(j\) are belong to same group, and takes 1 only if these vertexes are belongs to different groups. Hence, the maximum cut problem is formulated as \(\max \sum_{i < j} w_{i, j} (1 - s_i s_j)\), where \(w_{i, j}\) is the weight of edge \((i, j)\).

from flopt import *

G = networkx.Graph()
f = iter(data.split("\n"))
N, E = map(int, next(f).split()) # N is the number of vartexes, and E is the number of edges

# create spin variables
s = Variable.array("s", N, cat="Spin", ini_value=1)

# create objective function
obj = 0
for e in range(E):
    i, j, w = map(int, next(f).split())
    obj += w * (1 - s[i-1] * s[j-1])

# create problem
prob = Problem(sense=Maximize)
prob += obj

# solve
staus, log = prob.solve(solver="Random", timelimit=1)

print("result = ", Value(s))
>>> [-1 1 -1 -1 1]

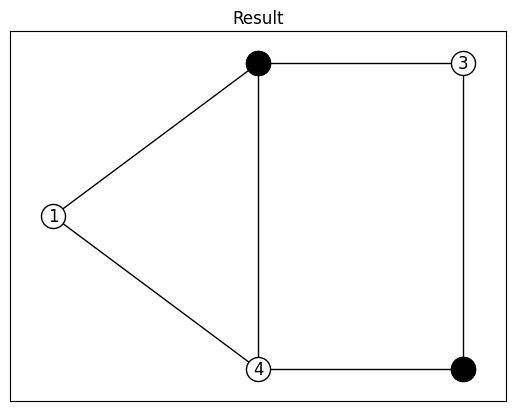
Plot the result partitioning.

# plot the graph
nodelist = [i+1 for i in range(N) if s[i].value() == 1]
networkx.draw_networkx_nodes(G, pos, nodelist=nodelist, node_color="black", ax=ax)
ax.set_title("Result")

Gset Benchmark

Gset is the benchmark the maximize cut problem. We can download the Gset benchmark as follows.

mkdir Gset && cd Gset; for i in {1..81}; do wget http://web.stanford.edu/~yyye/yyye/Gset/G$1; done

# select problem
file = "./Gset/G11"

from flopt import *

def loader(f, n):
    for i in range(n):
        yield map(int, next(f).split())

# load problem, and create spin variables and objective function
with open(file, "r") as f:
    N, E = map(int, next(f).split())
    s = Variable.array("s", N, cat="Spin")
    obj = 0.5 * Sum(w * (1 - s[i-1] * s[j-1]) for i, j, w in loader(f, E))

# create Problem
prob = Problem(sense=Maximize)
prob += obj

# select algorithm to search and solve
status, log = prob.solve(solver="Random", timelimit=10, msg=True)

Convert another formulations

We can obtain the data for the another formulation using flopt.convert, for example ising structure.

\(\min - x^T J x - h^T x + C\)

import flopt.convert

ising = flopt.convert.IsingStructure.fromFlopt(prob)
print(ising.J)
print(ising.h)
print(ising.x)

When you have the solution by your algorithm or other applications, you can input the value to the spin variable of flopt.

values = [...]  # solution; list of values
for var, value in zip(ising.x, values):
    var.setValue(value)